割り算をする前に、その計算が割り切れるかどうかを一目で見分ける方法を伝授しましょう。
ある数字が、3で割り切れるかどうかは、
すべての位の数字を合計し、その数が3で割り切れるかどうかで判別できます。
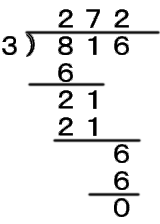
|
たとえば、816という数字が3で割り切れるかどうかを考えてみましょう。 |
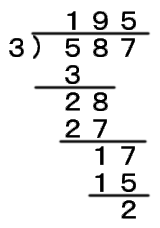
|
一方、587はどうでしょう? |
いくつか例を挙げましょう。
1282
各位の数字の和=1+2+8+2=13(3で割ると1あまる)
1282÷3=427あまり1
※この時、あまりは一致します。
837
各位の数字の和=8+3+7=18(3で割り切れる)
837÷3=279(割り切れる)
1116
各位の数字の和=1+1+1+6=9(3で割り切れる)
1116÷3=372(割り切れる)
次に「6」で割り切れる数の見分け方ですが、2×3=6ですから、
『「6」で割り切れる』ということは『「2」と「3」の両方で割り切れる』ということと同じです。
なので、
・偶数
かつ
・すべての位の数字の合計が「3」で割り切れる
ことが、「6」で割り切れるための条件となります。
たとえば、816という数は、偶数かつ各位の数字の合計は8+1+6=15なので「3」でも割り切れます。
ですから、816は「6」で割り切れる数字です。
実際に割り算をしてみると、816÷6=136となり、確かに割り切れます。
ある数が「9」で割り切れるかどうかは、
すべての位の数字を合計し、その数が9で割り切れるかどうかで判別できます。
たとえば1827は、各位の数字の合計=1+8+2+7=18で、これは9で割り切れますから、1827も9で割り切れます。
実際に割り算をすると、1827÷9=203となって、確かに割り切れています。
しかし937などは、各位の数字の合計=9+3+7=19で、これは9で割ると1あまり、割り切れません。
実際に、937÷9=106あまり1となって割り切れません。
なお、この時それぞれのあまりが一致していることは注目すべきポイントです。
以上をまとめると次のようになります。
「3」
各位の数字の合計が3で割り切れるとき、割り切れる
※あまりがある時は、そのあまりは一致する
「6」
偶数かつ
各位の数字の合計が3で割り切れるとき割り切れる
「9」
各位の数字の合計が9で割り切れるとき、割り切れる
※あまりがある時は、そのあまりは一致する
なお、そのほかの数字については有効な見分け方はありません。
続いて、大きな数の足し算をインド式で計算してみましょう。
インド式足し算へ≫