インド式３桁×３桁の掛け算

インド式数学・インド式算数を利用して３桁×３桁の掛け算を計算してみましょう。

今まで学んだ計算術と同様にして、３桁×３桁の掛け算もできます。

【３桁×３桁の掛け算の位取り】

１の位	１の位×１の位	cz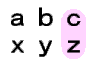
１０の位	１０の位×１の位 １の位×１０の位	bz cy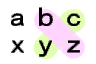
１００の位	１００の位×１の位 １０の位×１０の位 １の位×１００の位	az by cx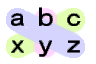
１０００の位	１００の位×１０の位 １０の位×１００の位	ay bx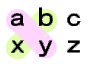
１００００の位	１００の位×１００の位	ax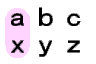

これより次の公式が得られます。
あとは、くり上がりに注意して足し合わせるのみです。

例：３８４×２９５
6｜27+16｜15+72+8｜40+36｜20
6｜  43 ｜   95  ｜  76 ｜20
＋ 　＋　　　＋　　　＋
5　　10　　　 7       2
―――――――――――――――
11　  3　　　 2　　　 8　　0

答：113280

例２：５２９×４３１
20｜15+8｜5+6+36｜2+27｜9
20｜ 23 ｜  47  ｜ 29 ｜9
＋ 　＋　　 ＋　　 ＋
 2　  4　　  2      0
―――――――――――――
22    7      9      9   9

答：227999

このようにインド式数学を使うことで、大きな数の掛け算もミスなく計算できるようになりました。
しかし驚くのはこれから。インド式数学を使えば、同じ数をかける（２乗する）場合などは、もっと計算が簡単になるのです。
インド式２乗の計算へ≫

Copyright (C)インド式数学で計算しよう since 2008

「インド式数学で計算しよう」は全ページリンクフリーです。サイト内の記事の無断引用を禁じます。