インド式数学で計算しよう>インド式掛け算>2乗の計算
同じ数をかける(2乗)の計算
インド式数学を使うと、同じ数をかける(2乗する)場合の計算がとても簡単になります。
1の位の数字が「0」の場合
この場合は簡単ですね。
10の位だけ掛け算をして、あとでお尻に0をつければ良いだけです。
例:40×40=4×4×100=16×100=1600
1の位の数字が「5」の場合
1の位の数字が「5」の場合を計算してみましょう。
やり方は単純。
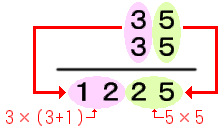
|
(1) 1の位×1の位を計算して書く (2) 10の位×(10の位+1)を計算して書く |
これぞインド式数学の本領発揮。
超簡単に答えが求まってしまいました。
1の位の数字が「5」の場合の2乗計算
a×(a+1)|b×b
解説
なぜ、こんな簡単に計算ができてしまったのでしょうか?
2桁×2桁の公式にあてはめてみましょう。
2桁×2桁の公式「ax|ay+bx|by」において、a=x=3、b=y=5としてみると
3×3|3×5+5×3|5×5
3×3| 3×(5+5) |5×5
3×3| 3×10 |5×5
9| 30 | 25
となり、3がくり上がるので答えは1205となります。
上の計算式をみてお分かりの通り、5は2倍すると10になるので、「ay+bx」の1の位がちょうど0になってくれます。
おかげで1の位の数字が「5」の時は、2乗の計算が暗算でも求められるくらいシンプルにできたのです。
しかし、インド式計算術の極意はこんなものではありません。
1の位の数字が「5」の場合を計算できると、1の位の数字が「4」や「6」の場合も簡単に2乗が計算できるのです。
インド式2乗の計算その2へ≫