インド式数学で計算しよう>インド式掛け算>3桁×2桁の掛け算
3桁×2桁の掛け算
今度はインド式数学で、3桁×2桁の掛け算を計算してみましょう。
2桁×2桁の掛け算のやり方さえ納得できれば、3桁×2桁や3桁×3桁の掛け算も簡単です。
(式は少し長くなりますが・・・)
まずはタテ書き筆算で計算してみます。
|
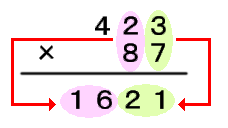
(1)筆算のように計算式をタテ書きします。 (2)「10の位×10の位」および「1の位×1の位」を計算して書きます。 |
|
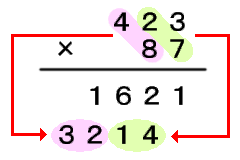
(3)「100の位×10の位」および「10の位×1の位」を計算して書きます。 |
|
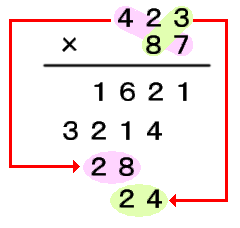
(4)「100の位×1の位」および「1の位×10の位」を計算して書きます。 |
|
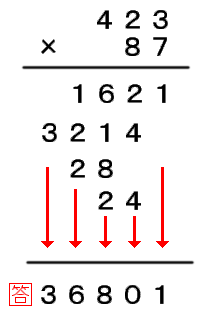
(5)2〜4を足し合わせれば答えです。 |
位どりさえ間違わなければ、簡単にできますね。
3桁×2桁の掛け算(横書き法)
今度は横書きで計算してみましょう。
最初に位どりについてまとめます。
abc×xyの形で書いた場合についても載せます。
| 1の位 | 1の位×1の位 | cy |
| 10の位 | 10の位×1の位 1の位×10の位 | by cx |
| 100の位 | 10の位×10の位 100の位×1の位 | bx ay |
| 1000の位 | 100の位×10の位 | ax |
これより3桁×2桁の掛け算公式は、次の形に書けます。
3桁×2桁の掛け算公式
ax|ay+bx|by+cx|cy
分かりやすいように順を追って計算してみましょう。
例として、324×78を考えます。
|
324×78 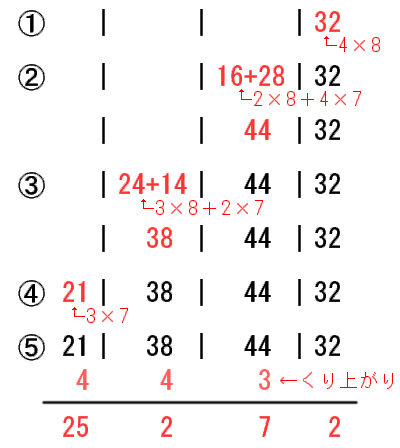
|
最初に桁区切りのためのタテ線を3本書いておきます。 (1)「1の位×1の位」を計算して一番右に書きます。 (2)「10の位×1の位」および「1の位×10の位」を計算して2番目に書きます。 (3)「100の位×1の位」および「10の位×10の位」を計算して3番目に書きます。 (4)「100の位×10の位」を計算して一番左に書きます。 (5)くり上がりを考えて足し合わせると答えです。 |
3桁×3桁の掛け算も同様にできます。
3桁×3桁の掛け算へ≫